My Work
I am interested in machine learning algorithms and how we can apply them to get the most out of our data. I am currently focused on applications of normalising flows to our Bayesian analysis pipelines and applications of machine learning algorithms to the calibration of radio antennas.
Below is a summary of some of my most recent work.
- Tensionnet: Calibrating tension statistics with neural ratio estimation
- Emulation and SBI Lectures
- Piecewise Normalizing Flows
- Joint Constraints on the first galaxies
- margarine: Marginal Bayesian Statistics
- Astrophysical constraints on the first galaxies from SARAS3
For a complete list of publications see here.
Tensionnet: Calibrating tension statistics with neural ratio estimation - 15102024
- Paper
- TLDR: Using Neural Ratio Estimation to calibrate out the prior dependence of Bayesian tension statistics.
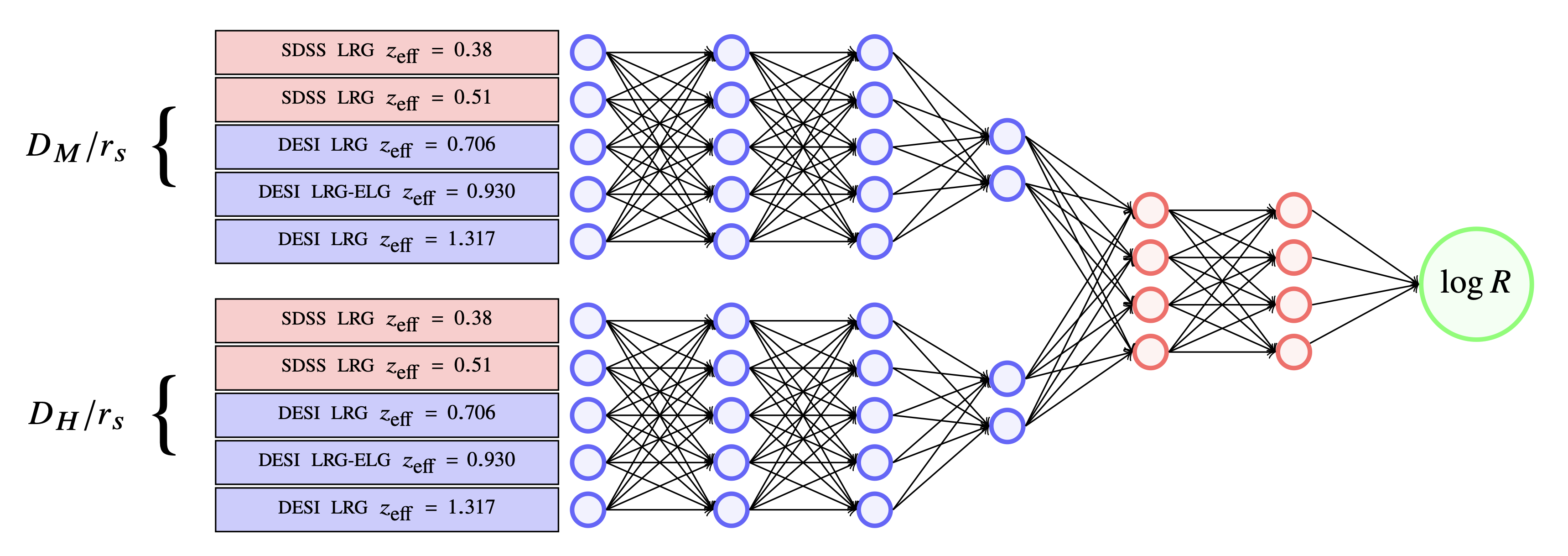
The paper proposes a new method to quantify the tension between different datasets that aim to measure the same physical parameters. This method utilizes a machine learning technique called Neural Ratio Estimation (NRE) to improve upon a traditional statistical measure of tension known as the evidence ratio, denoted as ‘R’.
In science, when two independent experiments measuring the same phenomenon yield results that disagree, we call it ‘tension’. This tension can point towards undiscovered physics, systematic errors in the experiments, or simply statistical fluctuations.
The evidence ratio ‘R’ is a Bayesian statistical tool that compares the likelihood of observing the combined data from two experiments under the assumption they agree (joint evidence) versus the likelihood of observing them if they are independent (product of individual evidences).
While R is a powerful tool, its interpretation depends heavily on the prior on the parameters of the model. The paper proposes using NREs to calibrate this prior dependence and create a new measure of tension called ‘T’, and a related measure of concordance called ‘C’.
This calibration method, termed TensionNet, uses NRE to predict the concordant distribution of R values by simulating matched and mismatched datasets. Once trained, the NRE converts the observed R value into a tension statistic T, expressed in standard deviations, and a concordance measure C.
The method involves:
- Simulation: Generating synthetic datasets where both datasets share identical underlying parameters (matched) or differ (mismatched).
- Training: Labeling these sets and training the NRE to classify them, optimizing using binary cross-entropy.
- Prediction: The trained NRE predicts the distribution of R under concordance. By comparing the observed R to this distribution, T and C are derived.
The paper demonstrates this method on a toy 21cm example and on observations of the Baryon Acoustic Oscillations from DESI and SDSS (see the figure below).
The tensionnet has several advantages. It helps to removes the subjective dependence on prior assumptions. ‘T’ allows for a more intuitive interpretation of tension in terms of standard deviations. NREs are computationally faster than traditional methods for calibrating ‘R’.
However, their are a few limitiations. For example the accuracy of this method depends on how well the simulations reflect the actual data and experimental uncertainties and the performance of the NRE. To use this method we also have to be able to simualte the observables we are interested in.
This paper presents a promising new technique using machine learning to more accurately quantify tension between datasets, with potential applications in cosmology and beyond.
Emulation and SBI Lectures
- Lecture One: Emulators
- Lecture Two: Simulation Based Inference
- TLDR: MPhil Data Intensive Science Minor Module lectures on the use of emulators and simulation based inference in astronomy and cosmology.
- 19/03/2024
I recently gave two lectures on the use of emulators and simulation based inference in astronomy and cosmology for the “Data Driven Radio Astronomy in the SKA Era” minor module for the Cambridge MPhil in Data Intensive Science. The lectures were non-examinable and designed to give the students an introduction to the application of machine learning tools in the field of Radio Astronomy. They followed a series of lectures covering a range of topics from electromagnetic modelling of array beams, imagining with interferometers and inference techniques given by members of the Cavendish Radio Cosmology Research Group.
In the first of my lectures I discussed how emulators allow us to physically model our data in computationally efficient ways that make Bayesian inference feasible. The likelihood function $L(\theta)$ in Bayesian inference is a function of our data model $M(\theta)$ where $\theta$ are physically meaningful parameters. In an MCMC chain the likelihood has to be called millions of times for different parameter sets but if our model is a semi-numerical or hydrodynamical simulation each call can take hours or even weeks making the inference infeasible. However, we can train neural network emulators with a comparatively small number of model realisations to accurately approximate the semi-numerical or hydrodynamical simulations. Typically these emulators will take fractions of a second to evaluate for a single parameter set reducing the likelihood evaluation time and making inference possible.
In the lecture I demonstrated how we build emulators for sky-averaged 21-cm Cosmology, discussed dimensionality reduction and discussed how one might emulate images with Convolutional Neural Networks. I wrote a set of example python notebooks demonstrating each of these concepts which are available here.
In the second lecture, I introduced Simulation Based Inference (SBI) and discussed why this is a useful tool in astrophysics and cosmology. In SBI the goal is to infer our likelihood from simulations of our observable and use neural networks to approximate the posterior $P(\theta|D)$, the likleihood $P(D|\theta)$ or the ratio of likelihood to Bayesian Evidence $\frac{P(D|\theta)}{P(D)}$. In the lecture I introduced the students to the concepts of Approximate Bayesian Computation, Neural Posterior Estimation with Conditional Normalising Flows and Neural Ratio Estimation. For each concept I again provided Python notebooks demonstrations (see here).

Piecewise Normalizing Flows
- Paper
- TLDR: Using clustering algorithms to improve the accuracy of normalizing flows when learning multi-modal distributions.
In this paper I demonstrated how we can exploit clustering algorithms to improve the accuracy of normalizing flows when learning highly multi-modal distributions.
Normalizing flows can be used to perform density estimation and are a bijective and differentiable transformation between a known base distribution and a target distribution. The transformation is often represented by a neural network that can be optimised to learn the target. Once learnt we can draw samples from the flow and calculate probabilities for a given set of samples on the distribution.
The flows typically struggle to learn multi-modal distributions because the topology of the base distribution is so different to the topology of the target distribution. A number of methods exist to improve the accuracy of flows on multi-modal distributions but we often find that the learned distributions feature bridges between the modes that are not present in the target.
In our work we showed that we can break the target distribution up into different clusters and train normalizing flows on each cluster. We discuss how to sample from this piecewise distribution and how to calcualte probabilities on it in the papaer.
The below figure shows how our piecewise normalizing flow approach performs in comparison to a single noramlizing flow (MAF) and an alternative approach detailed in Stimper et al. 2022.

Joint Constraints on the first galaxies
- Paper
- TLDR: Using a novel machine learning Bayesian workflow to derive joint constraints on the properties of the first galaxies with data from 21-cm cosmology experiments.
In this work we used normalizing flows to model posterior distributions from previous analysis of data from the 21-cm experiments SARAS3 and HERA to efficiently perform a joint analysis and place constraints on the properties of the first stars and galaxies.
21-cm cosmology is concerned with the detection of a signal from the Cosmic Dawn and Epoch of Reionization from neutral hydrogen which can inform us about the star formation rates of the first galaxies, their halo masses, their X-ray and radio luminosities and how quickly the universe ionized. We either attempt to detect the sky-averaged signal, redshifted from the early universe, in the radio band with single radiometers, like SARAS3, or detect the spatial variation in the signal through the power spectrum with interferometers like HERA.
Both HERA and SARAS3 have collected data in the past few years but neither experiment has claimed a detection of the signal. Instead they have been able to place upper limits on the magnitude of both the sky-averaged signal and the power spectrum. Using these upper limits we are able to demonstrate that we can recover tighter constraints on the magnitude of the signals and the properties of early galaxies than can be achieved with each experiment individually. The figure below shows the one-, two- and three-sigma constratints on the magnitude of the signals derived using the prior on our astrophysical parameters, from each experiment and jointly.

margarine: Marginal Bayesian Statistics
- Paper One
- Paper Two
- TLDR: Using normalizing flows to build of nuisance-free or marginal Bayesian workflow.
In these two papers we demonstrated that we could use normalizing flows to derive marginal posterior distributions, define marginal or nuisance-free likeilhood functions and calcualte marginal Bayesian statistics such as the Kullback-Leibler divergence and Bayesian Model Dimensionality.
We use normalizing flows, bijective and differentiable transformations between a base distribution and more complex target distribution, to post process MCMC and Nested Sampling chains and marginalise out nuisance parameters. This gives us access to the posterior distributions on core science parameters and allows us to evaluate probabilities without having to worry about instrumental nuiances and contaminating signals.
Through access to the marginal posterior distributions we then define the marginal Kullback-Leibler divergence and marginal Bayesian Model Dimensionality which allow us to evalute the constraining power of different experiments in just the core science part of the parameter space. In practice this allows us to compare different experimental approaches with different nuisance parameters and determine which is giving us the most information about the parameters that we are interested in.
Using the marginal or nuisance-free likelihood function we also outline a method for performing efficient joint analysis without having to sample the nuisance parameters but still recovering the correct Bayesian evidence. We demonstrated this with Planck and the Dark Energy Survey and the resultant joint constraints are shown below.
Astrophysical constraints on the first galaxies from SARAS3
- Paper
- Preprint
- Publisher: Nature Astronomy
- TLDR: The first constraints from 21-cm cosmology on the properties of the first galaxies 200 million years after the Big Bang.
In this work we used data from the SARAS3 radiometer to constrain the properties of galaxies at redshift of 20 roughly 200 million years after the Big Bang. The SARAS3 radiometer is aiming to detect the redshifted sky-averaged 21-cm signal from neutral hydrogen during the Cosmic Dawn and Epoch of Reionization. The signal, measured relative to the radio background, is sensitive to the star formation properties of the first galaxies, their X-ray and radio luminosities and the CMB optical depth.
Using an upper limit measurement of the signal from the SARAS3 instrument we are able to rule out scenarios in which high redshfit galaxies were very luminous in the radio band and had low X-ray efficiencies. We also place constraints on the star formation rate and minimum halo mass for star formation at high redshfits for the first time.
We compare our constraints to those from the precursor instrument SARAS2 and demonstrate that while the constraints are generally stronger from SARAS3 each experiment gives us information about the properties of galaxies at different redshifts. This suggests that we can gain information by performing a joint analysis of differnt data sets and is shown in the figure below. The figure shows the functional constraints on the 21-cm signal from each experiment against the prior and the KL divergence, a measure of the information gain when contracting the prior to the posterior, for each instrument.